|
Авторcтво: Меренкова Людмила Александровна, учитель математики МОУ «ООШ с. Мавринка Пугачевского района Саратовской области» |
При изучении математики школьники должны усвоить не только содержание знаний, но и способы их получения. Как же организовать обучение математике, чтобы усвоение математических понятий, аксиом, теорем, алгоритмов происходило в комплексе? Математическая деятельность не сводится лишь к воспроизведению полученных кем-то знаний, а включает в себя процесс поиска, открытия новых фактов и закономерностей. Выявление способов математической деятельности, состава познавательных средств, которые должны усваивать школьники и которые являются источником развития их интеллектуальных способностей, следует вести с позиции методологии научного поиска в математике.
Проследим путь познания в математической науке, который важен с точки зрения организации процесса познания математики школьниками. Он может быть представлен следующей схемой:

Для разработки технологии развивающего обучения учителю важно знать, какие методы
научного познания характерны для каждого этапа. Они могут быть отражены следующим образом:
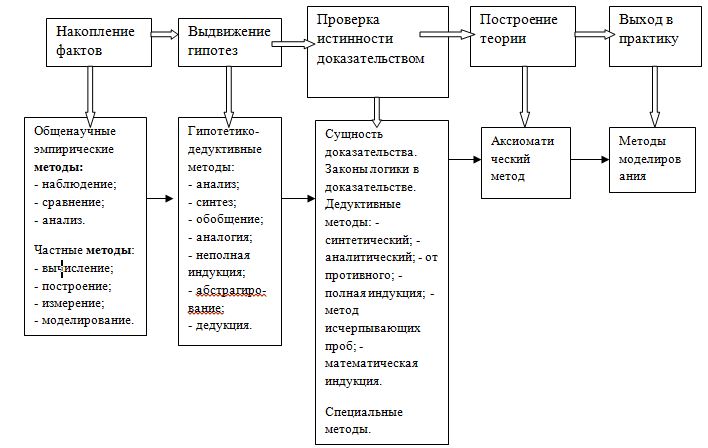
К числу эвристических методов науки прежде всего относятся наблюдение и сравнение, эксперимент и обобщение, неполная индукция, аналогия. Все эти методы позволяют выдвинуть гипотезы, которые требуют установления их истинности или ложности. К открытию математических фактов приводят и дедуктивные рассуждения. Эвристические методы науки позволяют включить учащихся в самостоятельный (управляемый учителем) поиск новых фактов, правил, формул, теорем.
Неполная индукция – это умозаключение, которое делается на основе рассмотрения некоторых фактов. Полученное таким образом умозаключение может быть только гипотезой. В курсе математики деятельность учащихся на выдвижение гипотез организуется через моделирование, измерение, вычисление, рассмотрение хорошо выполненных рисунков. Моделирование – подходящий прием при изучении такой темы, как «Площади многоугольников». Измерением целесообразно воспользоваться в теме «Признаки равенства треугольников», чтобы помочь учащимся сформулировать соответствующую гипотезу. Теорему Виета учащиеся могут «открыть» путем правильно направленных учителем вычислений. А вот то, что биссектрисы треугольника пересекаются в одной точке, ребята могут увидеть на чертеже.
Аналогия – в переводе с греческого означает «соответствие», «сходство». Аналогия часто позволяет «открыть» свойства фигур. Так, сравнивая определения средней линии треугольника и трапеции и доказав свойство средней линии треугольника, учитель с помощью соответствующей системы вопросов может побудить учащихся высказать гипотезу о свойстве средней линии трапеции.
Дедуктивные умозаключения. Заботясь о развитиимышления, важно в процессе обучения подводить школьников к «открытию» теорем на основе дедуктивных умозаключений. Например, изучение свойств прямоугольника можно начать таким вступлением: «Мы с вами изучили параллелограмм. Начали с определения, рассмотрели его свойства и признаки. Признаки выражены в теоремах, обратных соответствующим свойствам. А теперь постройте параллелограмм с прямыми углами и попытайтесь по аналогии с изучением параллелограмма построить теорию, связанную с его частным видом».
Для разработки технологии развивающего обучения важно учитывать и то, как происходит процесс усвоения. Педагогическая психология выделяет в этом процессе ряд последовательных этапов, прохождение каждого из которых является необходимым:

Важнейшей проблемой в обучении математике является развитие самостоятельности учащихся при решении текстовых задач, так как умение решать задачи является одним из основных показателей уровня математического развития школьников, глубины усвоения ими учебного материала. Но именно уровень самостоятельности учащихся при решении задач на сегодня оставляет желать лучшего. Например, в 6-ом классе многие учащиеся не справляются с решением такой задачи:
«В магазин привезли 600 кг муки. В первой половине дня продали ¼ всей муки, во второй половине дня – 2/5 остатка. Сколько муки осталось непроданной?»
Ошибочные решения в работах учащихся свидетельствуют о том, что ученики не смогли четко представить себе жизненную ситуацию, отраженную в задаче, не уяснили отношений между величинами в ней, зависимостей между данными и искомым, в результате чего выбирали непродуманные, случайные действия, механически манипулировали числами. В чем же главная причина слабых навыков учащихся при самостоятельном решении даже знакомых задач? Наблюдения, анализ письменных работ позволяют утверждать, что основная причина всех допускаемых детьми ошибок кроется в неправильной организации первичного восприятия задачи учащимися и ее анализа без должного уяснения жизненной ситуации, отраженной в задаче, и без ее графического моделирования. Уже в начальной школе каждый ученик должен уметь не только кратко записать условие задачи, но и проиллюстрировать условие с помощью рисунка, схемы или чертежа.
Однако даже в 5-6 классах, как правило, используются лишь разные виды краткой записи задачи да изредка готовые схемы, а создание модели задачи на глазах у детей, а тем более самими детьми, применяется крайне редко.
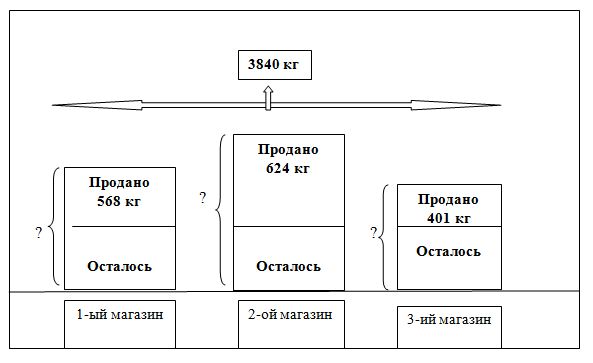
Что же понимается под моделированием задачи? Моделирование в широком смысле слова – это замена действий с обычными предметами действиями с их уменьшенными образцами, моделями, муляжами, макетами, а также с их графическими изображениями: условными знаками, рисунками, схемами, чертежами. Предметное и графическое моделирование при решении текстовых задач давно применяется в школьной практике, но без должной системы и последовательности, что объясняется неправильным применением роли наглядности при обучении математике учащихся средней школы. Наглядность, особенно графическая, нужна на всем протяжении обучения как важное средство развития более сложных форм конкретного мышления и формирования математических понятий. Рисунки, схемы и чертежи не только помогают учащимся в сознательном выяснении скрытых зависимостей между величинами, но и побуждают активно мыслить, искать наиболее рациональные пути решения задач, помогают не только усваивать знания, но и овладевать умениями применять их. Рассмотрим пример. Очень много ошибок 5-классники допускают в решении следующей задачи: «В три магазина привезли 3840 кг картофеля. После того как первый магазин продал 568 кг, второй – 624 кг и третий – 401 кг, картофеля осталось во всех магазинах поровну. Сколько кг картофеля получил каждый магазин?»
Варианты ошибочных решений:
|
I
|
II
|
III
|
|
1) 3840 – 568=3272 (кг)
2) 3840 – 624=3216 (кг)
3) 3840 – 401=3439 (кг)
|
1) 3840 : 3=1280 (кг)
2) 1280+568=1848 (кг)
3) 1280+624=1904 (кг)
4) 1280+401=1681 (кг)
|
1) 3840 – 568=3272 (кг)
2) 624 – 401=223 (кг)
3) 3272 – 223=3056 (кг)
|
Эти примеры показывают, что дети делали случайный, неосознанный и бездоказательный выбор арифметических действий. А вот если на глазах у детей и с их активным участием смоделировать эту же задачу в виде схемы, то такая модель поможет детям уяснить одно из важных условий задачи, которое вызвало наибольшие затруднения в решении, а именно что после продажи части картофеля во всех магазинах картофеля осталось поровну, т.е.одинаковое количество в каждом магазине.
В тексте задачи все данные и взаимоотношения между ними представлены описательно, раздельно, последовательно, а не одновременно, что не дает возможности ученику видеть сразу всю задачу в целом виде. А модель дала возможность детям видеть задачу в целом, одновременно воспринимать все ее данные и взаимоотношения между ними, между данными и искомыми. В результате большинство учащихся справляются с решением задачи. Модель создает условия для активной мыслительной деятельности учащихся в поисках разных способов решения одной и той же задачи и для обобщения теоретических знаний. А также именно модель помогает не только найти рациональный способ решения задачи, но и проверить его правильность. Рассмотрим это на примере еще одной задачи и модели к ней (6-ой класс): «Три группы учащихся очистили каток от снега. Первая группа очистила 7/12 катка, вторая – 2/3 того, что осталось, а третья – оставшиеся 250 м2. Вычислить площадь катка»
По предложению учащихся получилась следующая модель:

Анализируя модель, шестиклассники самостоятельно находят 2 способа решения задачи. В поисках различных способов решения задачи дети выясняют, какой способ решения является наиболее рациональным, и в то же время повторяют и закрепляют изученный теоретический материал.
Таким образом, использование графического моделирования при решении текстовых задач обеспечивает качественный анализ задачи, осознанный поиск ее решения, нахождение нескольких способов решения и выбор наиболее рационального из них и тем самым предупреждает многие ошибки в решении задач учащимися. Также модель задачи может быть использована для составления и решения обратных задач, для проведения исследования задачи, помогает установить условия, при которых задача имеет или не имеет решения, дает возможность учащимся сделать обобщение теоретических знаний.
Без осознания и оценки результата деятельности и самой деятельности, выявления ошибок и их причин урок математики не обеспечит требуемый уровень достижения цели.
Учение – это деятельность самоуправляемая, и вне этой позиции оно осуществляться не может. Именно этот момент требует обучения ученика умениям оценивать и анализировать свою деятельность, ее результаты и себя в этой деятельности. Организация учителем деятельности учащихся достигается сочетанием индивидуальной, парной, групповой работы учащихся, в которой ученик постоянно получает помощь в своей самостоятельной работе. Каждый из нас помнит, что решать задачи, готовиться к экзаменам легче вдвоем или втроем. У одноклассников проще спросить непонятное, получить консультацию, объяснить. Значит, надо организовать работу на уроке так, чтобы в нужный момент на помощь мог прийти одноклассник, чтобы можно было спросить, выяснить и чтобы не было страшно получить неудовлетворительную оценку. Этому способствует групповая форма работы. Группы организуются таким образом, чтобы имел место конфликт в социальном взаимодействии (конфликт – это противоречие в знании и незнании различных детей). Дети организованы в группы с разным уровнем развития: средний – низкий, высокий – средний. Тогда при наличии конфликта происходит развитие, т.е. качественные изменения. Каждый участвует в работе, вносит свой посильный вклад; сильный объясняет слабому, каждый поднимается на ступеньку выше. Абсолютно все ученики все полезное время тратят на достижение главной цели урока. Учитель только направляет работу, частично помогает, корректирует. При коллективной работе создаются следующие условия:
- понимание ученика и уважение к ученику (ученик чувствует себя значимым, полезным, с ним совещаются, разговаривают);
- помощь со стороны учащихся и учителя при необходимости (помощь незаметная, грамотная, посильная);
- каждый ученик в конце урока получает удовлетворительную оценку за свой труд.
Как же оценивается труд ученика при групповой работе? Существуют такие виды оценки: самооценка (с/о) и оценка группы (о/г). Ученик сам себе выставляет оценку за работу на каком-то этапе урока, критерий самооценки предлагает учитель. Оценка группы выставляется после обсуждения членами группы вклада каждого ученика при изучении какого-либо вопроса.
Учение – это целенаправленный и мотивированный процесс. Этому процессу способствует осознание учеником цели предстоящей деятельности. Для этого необходимо вносить новое в методы обучения и воспитания. Современный учитель должен:
· Переходить с позиций носителя знаний в позицию организатора собственной познавательной деятельности учащихся;
· Мотивировать познавательную деятельность ученика на уроке за счет коммуникации, взаимопонимания и добиваться либо интереса, либо устойчивого положительного отношения к предмету;
· Организовывать творческие и самостоятельные работы на уроке;
· Использовать коллективные способы обучения, включать всех учащихся в коллективную деятельность, организовывать взаимопомощь;
· Организовывать работу ученика с учеником или с источником знаний, помощь в деятельности ученику;
· Создавать ситуацию успеха, т.е. разрабатывать такое задание и такую методику, при которой ученик обязательно справится с работой;
· Организовывать гуманную систему взаимоотношений учитель – ученик, ученик – учитель при сочетании требовательности и уважения к личности;
· Организовывать самоанализ собственной деятельности ученика и ее самоанализ.
Организация процесса обучения связана с четким определением его целей. Целевые установки обучения делают для учащихся понятным смысл и способы организации учебно-познавательной деятельности и оказывают существенное влияние на ее активизацию.
Литература
1. Зверева Н.М., Касьян А.А. Методологические знания в содержании образования // Педагогика. 2001.
2. Методологические знания как основа развивающего обучения: Сб.статей /Отв.ред. Т.А.Иванова. Н.Новгород, 1999.
3. Глейзер Г.Д., Черкасов Р.С. Центр творческих усилий педагогов //Математика в школе. 2006.
Поделиться:

